L4: Analiza eksploracyjna zbioru danych

L4: Analiza eksploracyjna zbioru danych#

Exploratory data analysis (EDA)#

Przed rozpoczęciem rozwiązywania problemu przy użyciu metod uczenia maszynowego, w szczególności przed rozpoczęciem budowania modelu, konieczne jest sprawdzenie, z jakimi danymi przyszło się nam mierzyć.

Wśród podstawowych kwestii, które powinniśmy sprawdzić, są:

ile mamy cech?
które spośród nich to cechy kategoryczne, a które numeryczne?
jakie wartości przyjmują poszczególne cechy?
czy wśród danych są brakujące wartości?
czy istnieje i jak wygląda etykieta? (w szczególności - czy mierzymy się z zadaniem klasyfikacji, regresji czy klasteryzacji?)
czy dane są zbalansowane względem danej wyjściowej?

Dla małych i prostych zbiorów do nauki (tzw. toy tasks), zazwyczaj wystarczające jest ręczne przejrzenie pliku z danymi, by potrafić odpowiedzieć na w/w pytania. Niemniej przy bardziej ambitnych zadaniach, z pomocą przychodzą narzędzia automatyzujące pracę.

Przykładowy zbiór danych#

Przeanalizujmy klasyczny zbiór danych dotyczący wina (opublikowany przez Forina, M. et al, PARVUS - An Extendible Package for Data Exploration, Classification and Correlation. Institute of Pharmaceutical and Food Analysis and Technologies, Via Brigata Salerno, 16147 Genoa, Italy, więcej informacji tutaj)

Zbiór zawiera właściwości fizykochemiczne różnych próbek wina pobranych z jednego z regionów słonecznej Italii, jednakże pochodzących od trzech różnych plantatorów. Założeniem problemu jest określenie, który z nich jest wytwórcą danej próbki.

W celu uczynienia przykładu ambitniejszym, zbiór został celowo zaszumiony - tj. usunięto losowo część wartości.

Zacznijmy od wczytania zbioru:

import pandas as pd

df = pd.read_csv(
    "../docs/lab4/wine_with_nulls.csv",
)
df.head()

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline
0	14.23	1.71	2.43	15.6	127.0	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065.0
1	13.20	1.78	2.14	11.2	100.0	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050.0
2	13.16	2.36	2.67	18.6	101.0	NaN	3.24	0.30	2.81	5.68	1.03	3.17	1185.0
3	14.37	1.95	2.50	16.8	113.0	3.85	NaN	0.24	2.18	7.80	0.86	3.45	1480.0
4	13.24	2.59	NaN	21.0	118.0	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735.0

Na pierwszy rzut oka możemy stwierdzić, że wszystkie kolumny są numeryczne, ale ich wartości różnią się dość znacząco.

Podstawowe informacje o statystykach zbioru danych możemy uzyskać przy wbudowanej w Pandas metodzie describe()

df.describe()

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline	target
count	171.000000	170.000000	170.000000	167.000000	169.000000	171.000000	167.000000	171.000000	173.000000	170.000000	175.000000	170.000000	172.000000	178.000000
mean	13.009357	2.318059	2.360000	19.404790	100.088757	2.291988	2.019760	0.365614	1.583295	5.009529	0.959920	2.615176	756.209302	0.938202
std	0.819951	1.108406	0.275004	3.328986	14.490898	0.626310	1.006122	0.123074	0.572402	2.292621	0.228525	0.706861	315.609153	0.775035
min	11.030000	0.740000	1.360000	10.600000	70.000000	0.980000	0.340000	0.130000	0.410000	1.280000	0.480000	1.270000	278.000000	0.000000
25%	12.370000	1.575000	2.202500	17.150000	88.000000	1.730000	1.095000	0.270000	1.250000	3.220000	0.785000	1.970000	508.000000	0.000000
50%	13.050000	1.850000	2.360000	19.400000	98.000000	2.350000	2.170000	0.340000	1.540000	4.640000	0.980000	2.780000	679.000000	1.000000
75%	13.700000	3.030000	2.547500	21.500000	108.000000	2.800000	2.885000	0.445000	1.950000	6.122500	1.120000	3.177500	996.250000	2.000000
max	14.830000	5.800000	3.230000	30.000000	162.000000	3.880000	5.080000	0.660000	3.580000	13.000000	1.710000	4.000000	1680.000000	2.000000

Wykresy z użyciem metod Pandas#

Pandas udostępnia prosty interfejs rysowania wykresów Matplotlib bezpośrednio z DataFrame. Dzięki temu możemy prościej zwizualizowac wartości numeryczne i zaobserwować charakterystykę zbioru danych.

df = df[["alcohol", "ash", "total_phenols"]]

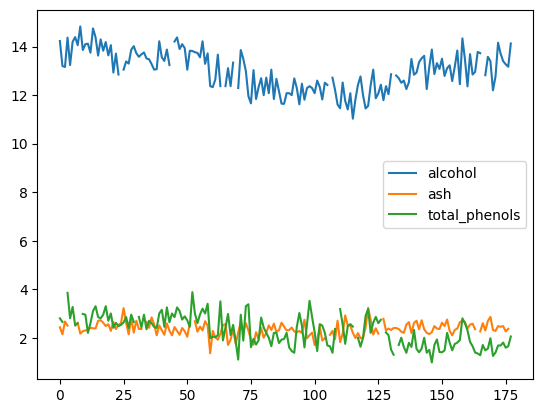
df.plot()

<Axes: >

../_images/c21c9c66b9fd5bbd4eb6248c8f90c0633cc104652b3cb054f2409eb7dbaabbe6.png

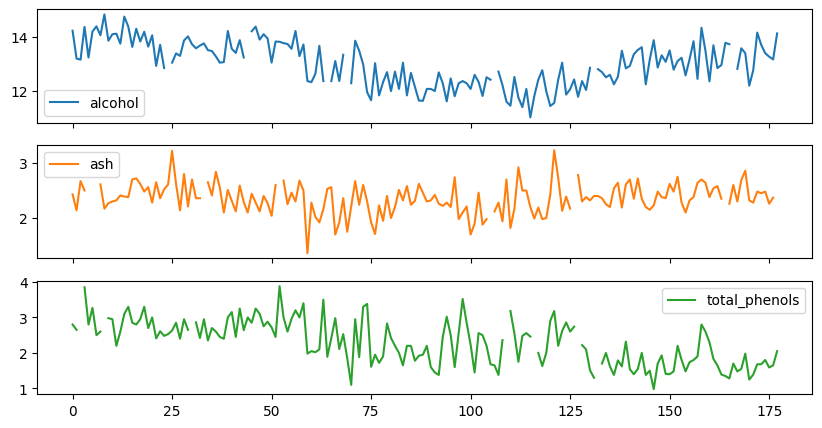
df.plot(subplots=True, figsize=(10, 5))

array([<Axes: >, <Axes: >, <Axes: >], dtype=object)

../_images/a8b7c9674152cb1ecbb415f903a43a0cb5a69190b07fdaed3ab97fbfc085fa26.png

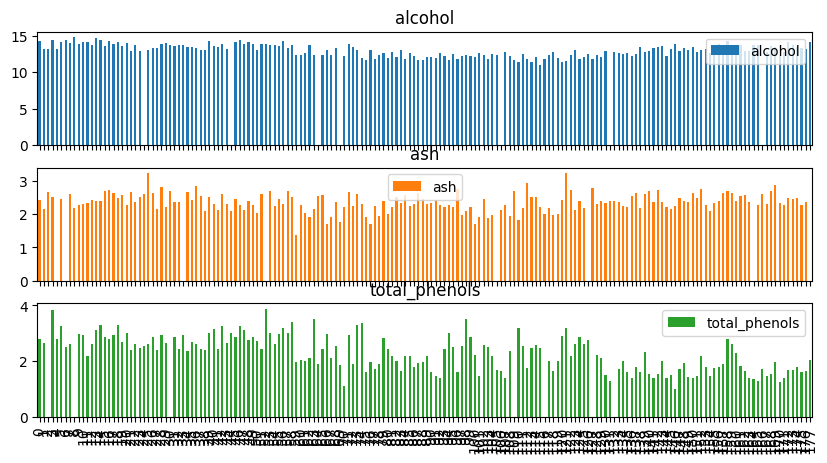
df.plot(kind="bar", subplots=True, figsize=(10, 5))

array([<Axes: title={'center': 'alcohol'}>,
       <Axes: title={'center': 'ash'}>,
       <Axes: title={'center': 'total_phenols'}>], dtype=object)

../_images/ef5c5cc277f037c71f8c0cd06c42181c8caa87f617a05b07e0c6dd3f52957c6e.png

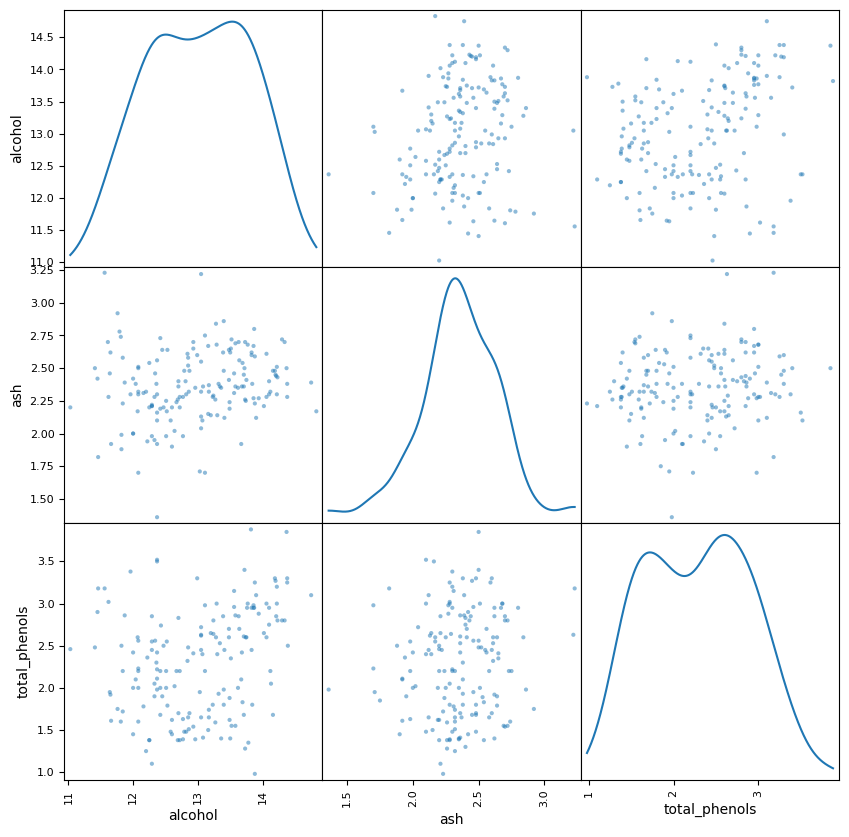
from pandas.plotting import scatter_matrix

scatter_matrix(df, alpha=0.5, figsize=(10, 10), diagonal="kde")

array([[<Axes: xlabel='alcohol', ylabel='alcohol'>,
        <Axes: xlabel='ash', ylabel='alcohol'>,
        <Axes: xlabel='total_phenols', ylabel='alcohol'>],
       [<Axes: xlabel='alcohol', ylabel='ash'>,
        <Axes: xlabel='ash', ylabel='ash'>,
        <Axes: xlabel='total_phenols', ylabel='ash'>],
       [<Axes: xlabel='alcohol', ylabel='total_phenols'>,
        <Axes: xlabel='ash', ylabel='total_phenols'>,
        <Axes: xlabel='total_phenols', ylabel='total_phenols'>]],
      dtype=object)

../_images/e86a6110735206ef55da20a8be5950e69e2aaf305028bbda1db2a9eab73eb0d1.png

Ydata-profiling#

Ydata-profiling (w przeszłości pandas-profiling) - biblioteka automatycznie analizująca zbiór danych i generujaca interaktywny raport. Alternatywnie, raport można zapisać w formacie .html

Instalacja przebiega standardowo:

pip install ydata-profiling

Użycie biblioteki jest niezwykle proste:

from ydata_profiling import ProfileReport

df = pd.read_csv(
    "../docs/lab4/wine_with_nulls.csv",
)

profile = ProfileReport(df)
profile.to_notebook_iframe()

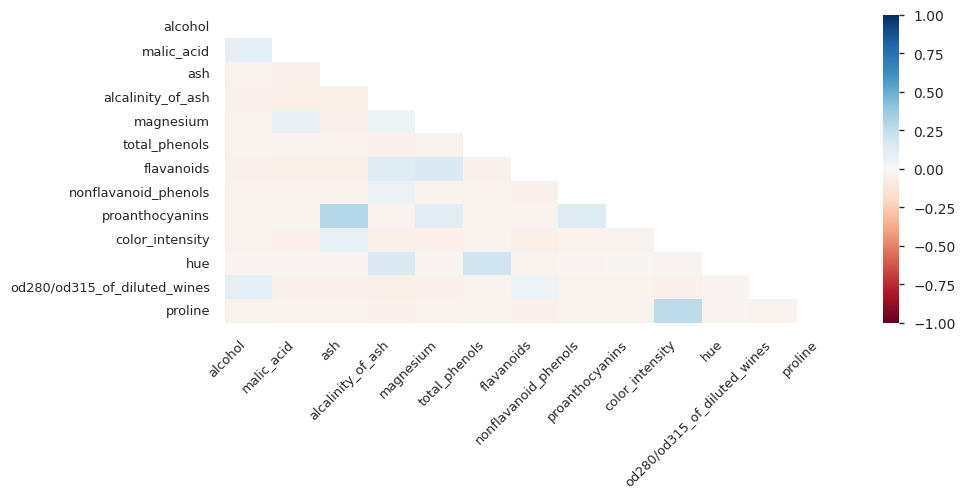
../_images/0de642c6db6cb541f9b0266416df9f3868bd0503e8ea0de9d346098c7cfabf22.png

Z raportu dowiadujemy się między innymi:

mamy 13 kolumn numerycznych (dane wejściowe), jedną kategoryczną (etykieta) - będziemy więc zajmować się klasyfikacją
klasy są całkiem nieźle zbalansowane (39%, 33%, 27%)
mamy kolumny z pustymi wartościami
możemy dokładnie przeanalizować statystyki poszczególnych cech, ich histogramy oraz wykresy zależności pomiędzy nimi

Redukcja wymiarowości jako element EDA#

W przypadku dużej ilości wymiarów danych, przydatne stają się metody redukcji wymiarowości. Pozwalają one mn. zmniejszyć ilość danych koniecznych do przeanalizowania, poprzez przekształcenia wartości pokazując zależności danych.

Dzięki metodom redukcji wymiarowości mamy możliwość wizualizacji całego zbioru danych w 2D lub 3D - w przeciwnym wypadku, analizując wykresy pojedynczych kolumn lub zalezności pomiędzy dwoma kolumnami (np. scatter matrix z Pandasa), nie mamy pełnego oglądu na całość datasetu.

Analiza głównych składowych (ang. Principal Components Analysis - PCA)#

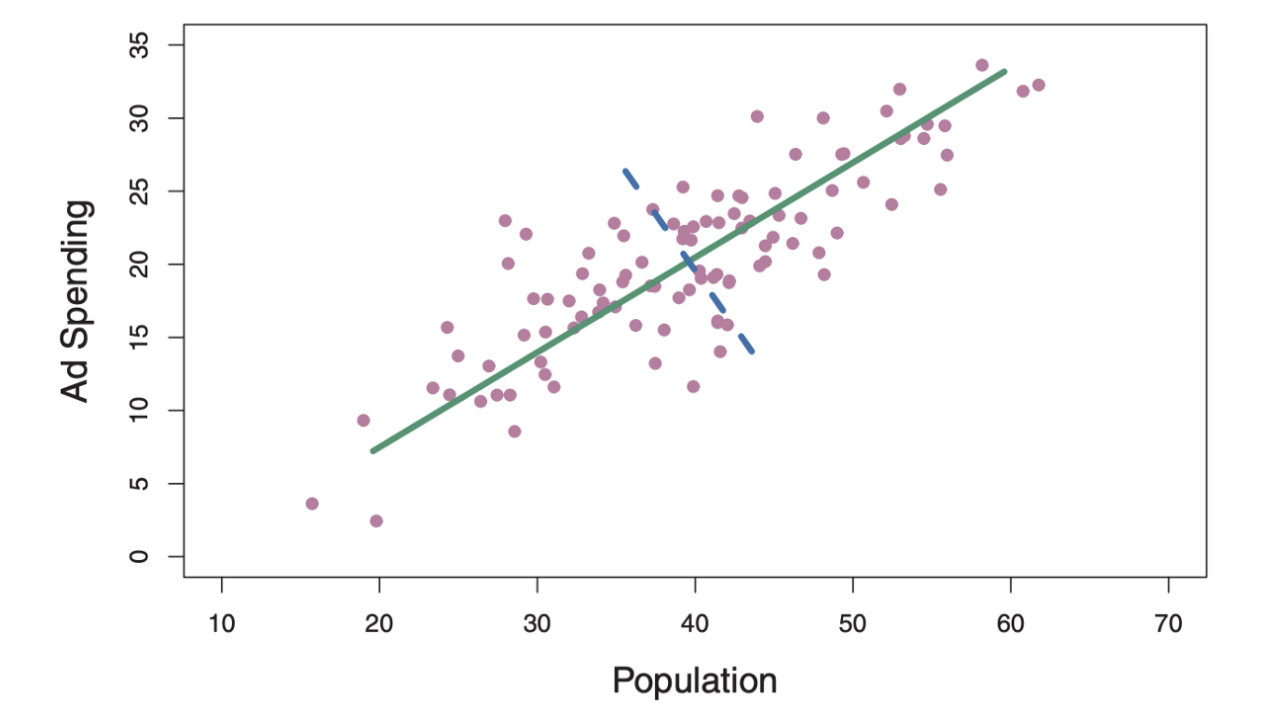
Najpopularniejsza metoda redukcji wymiarów. Dzięki modyfikacjom układu współrzędnych, stara się maksymalizować wariancję danych pierwszych wymiarów.

Przykładowe działanie:

Przykład użycia PCA#

# PCA nie przyjmuje brakujących wartości - wczytamy więc pełnowymiarową wersję datasetu wine, dla uproszczenia
from sklearn.datasets import load_wine

loaded_wine = load_wine(as_frame=True)


# PCA jest wrażliwe na skalę wartości poszczególnych cech - zeskalujemy je więc

from sklearn.preprocessing import StandardScaler

# separujemy cechy od targetu
x = loaded_wine["data"].values
y = loaded_wine["target"].values

# i standaryzujemy wartości cech
x = StandardScaler().fit_transform(x)
#
# dokonujemy analizy PCA do 2 wymiarów
#
from sklearn.decomposition import PCA

pca = PCA(n_components=2)
transformed = pca.fit_transform(x)

principal_df = pd.DataFrame(data=transformed, columns=["component 1", "component 2"])
pca_df = pd.concat([principal_df, loaded_wine["target"]], axis=1)

#
# wizualizujemy przekształcony zbiór
#
import matplotlib.pyplot as plt

plt.xlabel("Principal Component 1", fontsize=15)
plt.ylabel("Principal Component 2", fontsize=15)
plt.title("2 component PCA", fontsize=20)
targets = loaded_wine.target.unique()
colors = ["r", "g", "b"]

for target, color in zip(targets, colors):
    indices_to_keep = pca_df["target"] == target
    plt.scatter(
        pca_df.loc[indices_to_keep, "component 1"],
        pca_df.loc[indices_to_keep, "component 2"],
        c=color,
    )
plt.legend(targets)
plt.grid()

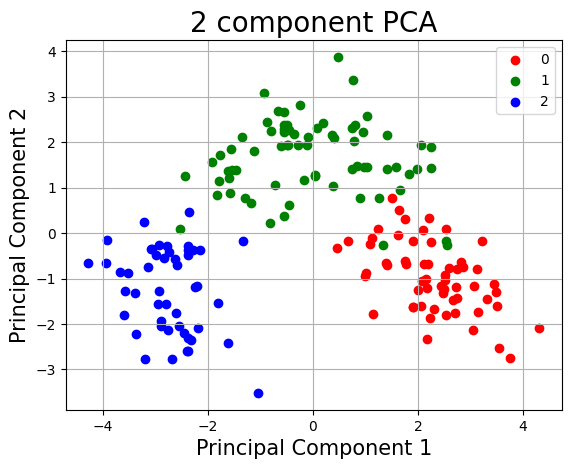
../_images/e10fb1357d5659c90c65cc8892b6881b521aaca37327bfc9ff92906099dc0a1b.png

Dokonując metody redukcji wymiarowości, tracimy część informacji zawartych w danych. Badając rozkład wariancji względem komponentów, możemy zbadać efektywność redukcji wymiarów - a co za tym idzie, oszacować na ile możemy polegać na wynikach PCA

pca.explained_variance_ratio_

array([0.36198848, 0.1920749 ])

pca2 = PCA(n_components=13)
transformed = pca2.fit_transform(x)
pca2.explained_variance_ratio_

array([0.36198848, 0.1920749 , 0.11123631, 0.0706903 , 0.06563294,
       0.04935823, 0.04238679, 0.02680749, 0.02222153, 0.01930019,
       0.01736836, 0.01298233, 0.00795215])

import numpy as np

plt.plot(np.cumsum(pca2.explained_variance_ratio_))
plt.xlabel("number of components")
plt.ylabel("cumulative explained variance");

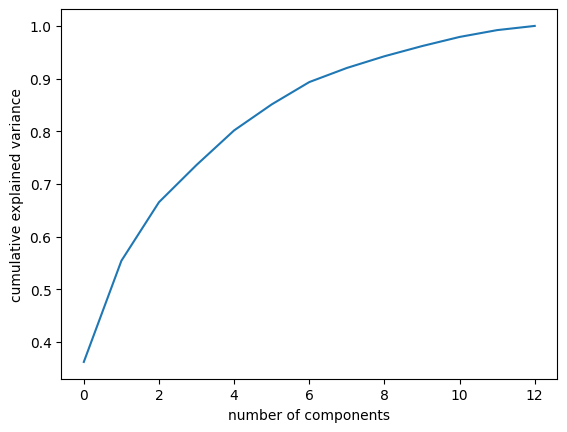
../_images/77afda6ae1461ab25a4694c51d10ed5f5d1016d4f14fae4891a95557bff8e8f0.png

Używając jedynie dwóch wymiarów, gromadzimy ponad 55% wariancji informacji zawartych w bazowych 13 wymiarach danych. Wynik nie powala na kolana, ale wizualizacja pokazuje że powinno to być wystarczające by stwierdzić, że nasz zbiór danych jest separowalny

EDA danych tekstowych#

Wyżej przedstawione metody działają w przypadku zbiorów zawierających dane numeryczne, w szczególności ciągłe. W przypadku danych tekstowych, do uzyskania wstępnego zrozumienia danych które mamy obrabiać może służyć np. wizualizacja częstotliwości pojawiających się słów.

from sklearn.datasets import fetch_20newsgroups

newsgroups = fetch_20newsgroups(
    subset="train",
    categories=["alt.atheism", "sci.space"],
    remove=("headers", "footers", "quotes"),
)

newsgroups_df = pd.DataFrame(newsgroups["data"], columns=["text"])
newsgroups_df["target"] = pd.Series(newsgroups["target"])
newsgroups_df["target"] = newsgroups_df.apply(
    lambda x: "alt.atheism" if x["target"] == 0 else "sci.space", axis=1
)
newsgroups_df.head()

	text	target
0	: \n: >> Please enlighten me. How is omnipote...	alt.atheism
1	In <19APR199320262420@kelvin.jpl.nasa.gov> baa...	sci.space
2	\nHenry, I made the assumption that he who get...	sci.space
3	\n\n\nNo. I estimate a 99 % probability the Ge...	sci.space
4	\nLucky for them that the baby didn't have any...	alt.atheism

import seaborn as sns
import nltk
from nltk.corpus import stopwords

stop = stopwords.words("english")

newsgroups_df["tokenized_text"] = newsgroups_df["text"].str.lower().str.split()

df_exploded = (
    newsgroups_df.explode("tokenized_text")
    .reset_index(drop=True)
    .rename(columns={"tokenized_text": "word"})
)
df_exploded = df_exploded[~df_exploded["word"].isin(stop)]

plt.figure(figsize=(10, 10))
sns.countplot(
    y="word",
    data=df_exploded,
    order=df_exploded["word"].value_counts().iloc[:20].index,
    hue="target",
)
plt.xticks(rotation=90)
plt.show()

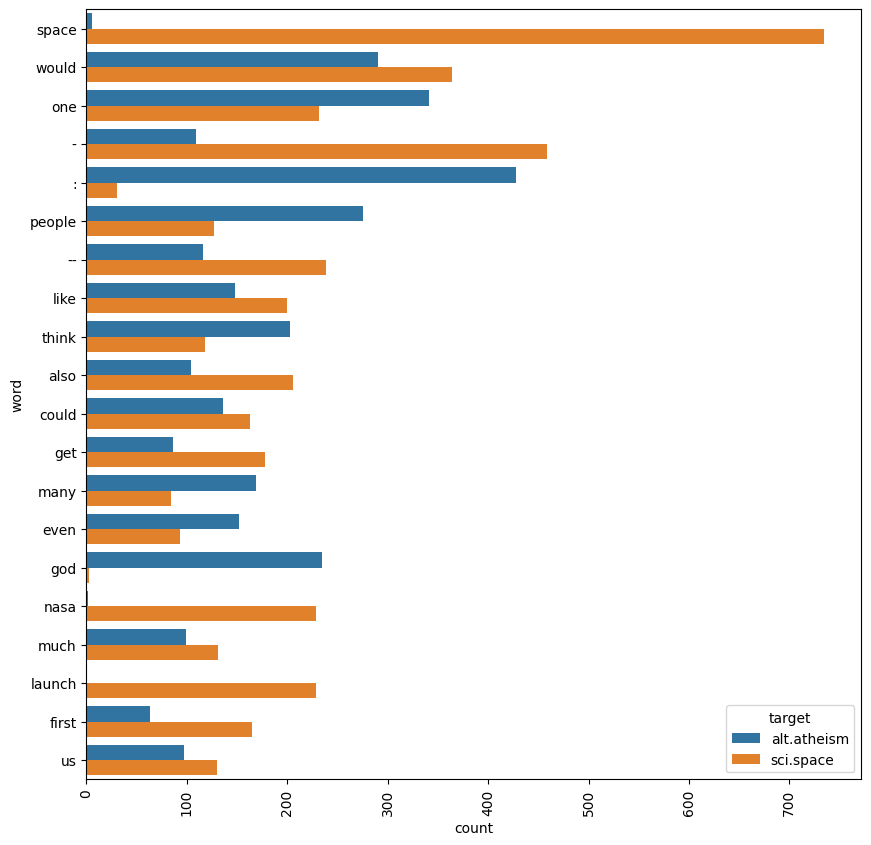
../_images/4ed119df79eb43f77b2324a1ea3ad6ad06e5dcb15ea05fe73652034fbc7ce5d0.png

Hint

Powyższy przykład zakłada taką samą ilość tekstu dla każdej z kategorii. W rzeczywistym przypadku należy liczbę wystąpień znormalizować.